Vol.6　斜面の原理

今回は「斜面の原理」についてお話します。
（vol.3）の記事にも掲載しましたが、紀元前2600年にピラミッドを建設した際は、「ねじの生命」とも言われる「斜面の原理」が使われています。
ピラミッドは230万ヶの石を積み上げて建設されたそうです。
その石を切り出し、運び、積み上げる人間が、どれくらい投入されたのか？実は、3ヶ月に10万人の割合で各地から人を集めて、23年掛かって完成したそうです。
中国の万里の長城も、同じだったと想像されます。
大陸的な、なにか時間がゆったり流れていくようなロマンが感じられますが、当時の人は、それ所ではなかったでしょう。
重い石を移動し積み上げるのには、ロープなどで持ち上げるのが一番簡単ですが、当時としては困難でした。
そこで「斜面」を利用した方法を考えました。
ちょっと数学が苦手の人にはイヤな図が載っていますが、辛抱して見てください。

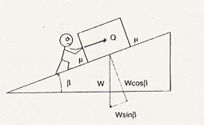
（図1 斜面の原理）

重さ（Ｗ）の石を持ち上げるのにはロープなどを使うと（Ｗ）と同じ以上の大きさの力が必要です。
何トンもの石だと不可能です。
そこで図1のように斜面を使いますと、重さ（Ｗ）の石は、斜面に押しつけられる力Wcosβと、斜面に沿ってずり落ちようとする力Wsinβに分解されます。
ですから、石を押している人は、この二つの力よりわずかに大きい力（Ｑ）を出せば、石は坂の上に移動します。
実際の作業には石と坂との摩擦も追加する必要がありますが、押し上げるのに必要な力はQ＞Wsinβ+μ･Wcosβとなります（μは摩擦係数です）。

摩擦係数μを一定とすれば、斜面（坂）の傾きが緩いほど、人が押す力Qは小さくて済みます。
（ピラミッド建設時は、このμを小さくするため、石の下に丸い木を入れて、点接触で軽く転がしたのでしょう）ねじはこの「斜面の原理」を応用して、緩い斜面を、円筒に巻き付けた物です。

仮想的な円筒をJISでは「有効径」ｄ2斜面の傾きを「リード角」β円筒に巻き付けた斜面を「つる巻線」「リード角」に沿って円筒を一巻きする間に進む距離を「リード」Iと言い、隣同士の「つる巻線」の間隔を「ピッチ」Ｐと言います、「つる巻線」は一本とは限りません、二本、三本と多数あるねじも存在します。

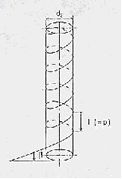
（図2 仮想的な円筒）

図2でリードI=ピッチPの場合は一条ねじリードI=2ピッチ2Pの場合は二条ねじリードI=8ピッチ8Ｐの場合は八条ねじといいます。
過去に八条ねじを作ったことがありますが、ねじを一回転させると8ピッチ進みます（当たり前ですが）一回転させるだけで凄い距離が稼げます。
初めての経験で驚いたものです。

今回は、多少判りにくかったかと反省してますが、これがねじの基本です。
（閑話休題）数学が苦手な人に、ちょっとだけ数字に（売上ではないですよ）興味がでる問題。計算機を使ってやってみてください。
1割る9，2割る9，3割る9・・・・1割る7、2割る7、3割る7・・・・以外と面白い数字がでてきますよ。

著者：株式会社ヤマシナ